1. KDE（カーネル密度推定）の基礎

カーネル密度推定(Kernel Density Estimation, KDE) は与えられたデータから、その下にある未知の確率密度関数を推定するノンパラ手法。

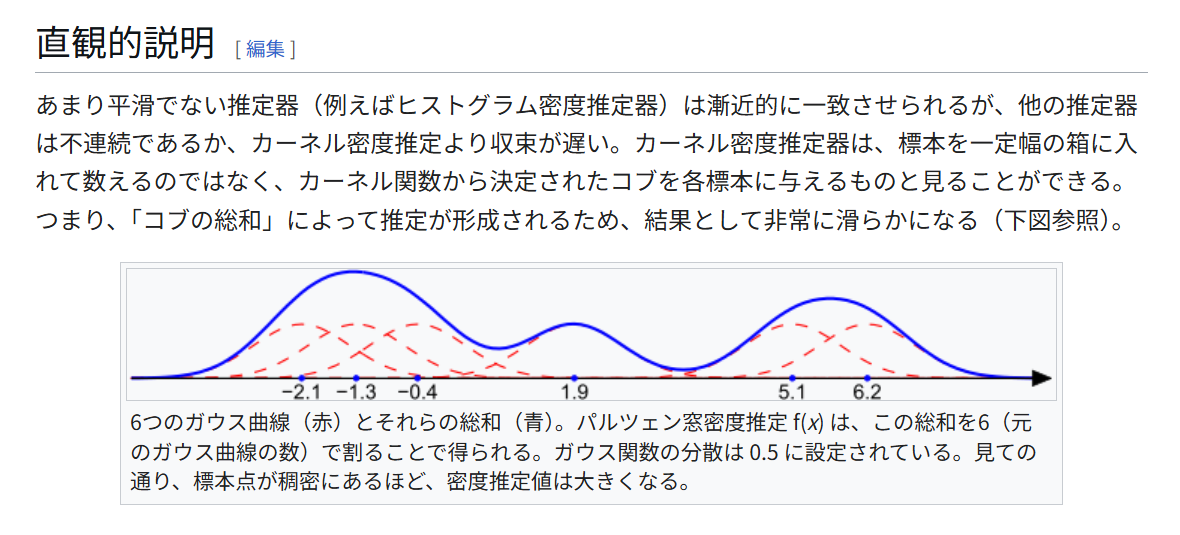
ヒストグラムのようにビンにデータ点を数える代わりに、各データ点の近傍になめらかな「カーネル関数」（例えばガウス関数）による山（コブ）を配置し、それらを重ね合わせることで全体の密度関数を推定する。

KDEの数式表現は次の通り。データ点を $x_1, x_2, \dots, x_n$ とし、カーネル関数を $K$, バンド幅(平滑化パラメータ)を $h$ とすると、ある点 $x$ での推定密度 $\hat{f}_h(x)$ は以下で与えられる。

$$\hat{f}_h(x) = \frac{1}{nh}\sum_{i=1}^n K\left(\frac{x-x_i}{h}\right)$$

この式では、各データ点 $x_i$ について、その周りに幅 $h$ のカーネル関数 $K$ を置き、データで平均を取る。典型的には、ガウス核(Gaussian kernel) と呼ばれる標準正規分布(平均0, 分散1のガウス関数)

$$K(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2}$$

をカーネルに採用することが多い。

こうすることで、 $\hat{f}_h(x)$ はガウス分布の重ね合わせ(混合分布)として計算され、データ点が密集している領域では多くのカーネルが重なるため高い密度推定値が得られ、データがまばらな領域では密度が低く推定される。

直感的には、各データ点が「小さな山」を形成し、その山の総和が確率密度の推定結果になる。

引用: カーネル密度推定, Wikipedia

2. GDKDEとは

GDKDE(Gradient Descent and KDE)は、ラプラシアンカーネルを用いた密度推定を攻撃アルゴリズムに組み込むことで、より「自然な」攻撃を行うものである。

勾配降下法(Gradient Descent)による最適化の文脈では、攻撃者はある損失関数 $F(\mathbf{x})$ を最小化するためにマルウェアサンプル $\mathbf{x}$ を段階的に更新していく。マルウェア検知回避のための基本的な損失関数は、モデルが出力する「マルウェアであるスコア」を表す関数 $g(\mathbf{x})$ (この値が大きいほどマルウェアらしいことを示す, SigmoidやLogitなど)を低減させることが目的になる。

しかし、$g(\mathbf{x})$ だけを最小化すると、しばしば決定境界の「穴」のような低密度領域（すなわち局所最小値）にサンプルが移動し、不自然な特徴を持つサンプルになってしまう恐れがある。そこでGDKDEでは、損失関数に密度ペナルティ項を追加し、サンプルがクリーンウェアデータの高密度領域から極端に外れないように誘導する。

Attack Strategy

攻撃者の最適な攻撃戦略は、マルウェアサンプル $\mathbf{x}^0$ に対し、$g(\cdot)$ またはその推定値 $\hat{g}(\cdot)$ を最小化するサンプル $\mathbf{x}^*$ を見つけることである。ただし、 $\mathbf{x}^*$ は $\mathbf{x}^0$ からの距離が、以下の制約を満たす必要がある。

$$\mathbf{x}^* = \arg \min_{\mathbf{x}} \hat{g}(\mathbf{x}) \tag{1} \\ \text{s.t. } d(\mathbf{x}, \mathbf{x}^0) \leq d_{\max}.$$

一般にこれは非線形最適化問題となる。これを解く方法として勾配降下法を用いる。しかし、$\hat{g}(\mathbf{x})$ は非凸関数である可能性があり、勾配降下法では大域的最適解に到達できない場合がある。

代わりに、降下経路が平坦な領域（局所最小値）に到達する可能性がある。これはサンプルの支持の外側、すなわち$p(\mathbf{x} \approx 0)$ の領域にある場合である。この場合、攻撃サンプルが回避成功するかどうかは 未サポート領域における $g$ の振る舞いに依存してしまい、成功を確信できない。

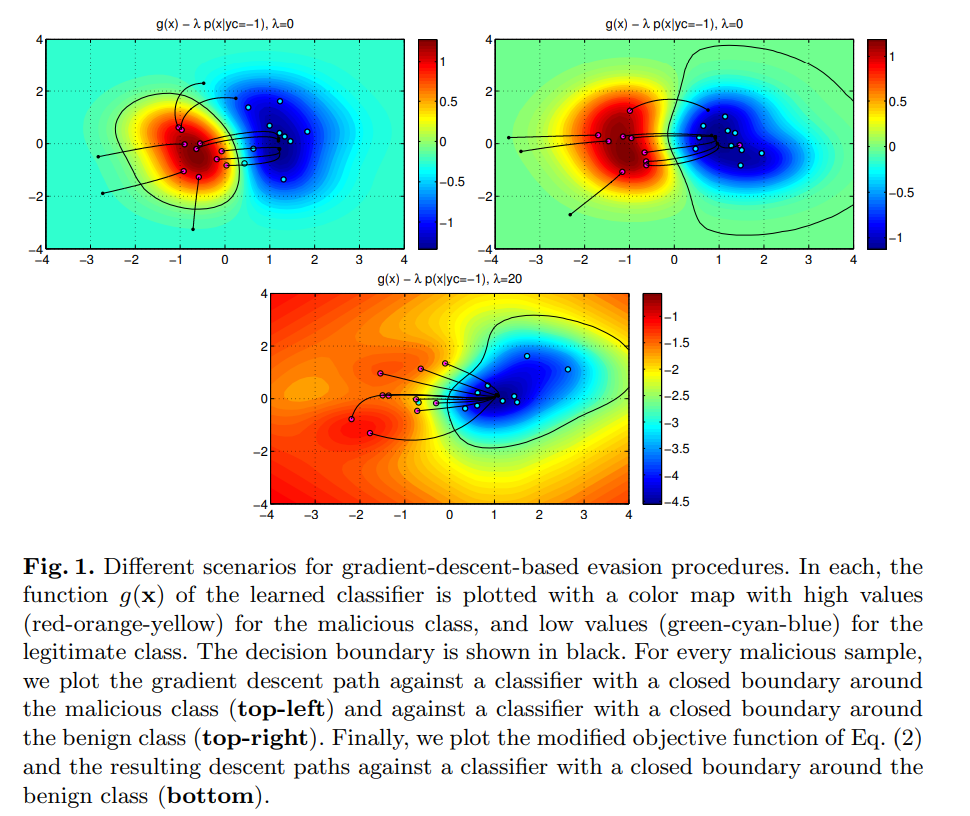
引用: Evasion attacks against machine learning at test time(2013)

このために、攻撃者が回避成功の確率を高めるには、クリーンウェアが密集する領域から攻撃ポイントを選択すべきである。こうした領域では $\hat{g}(\mathbf{x})$ の推定値がより信頼度高く（実際の$g(\mathbf{x})$に近づく）、その値は負の方向に向かう傾向がある。

この欠点を克服するため、攻撃目的(loss)関数に追加の要素し、次の目的(loss)関数を定義する。

$$F(x) = g(x) - \lambda p(\mathbf{x} \mid y^c = \text{cleanware})$$

ただし、$\lambda \ge 0$ はトレードオフを調整するハイパーパラメータである。第一項 $g(x)$ は「サンプル $\mathbf{x}$ がマルウェアと判定される傾向」を表し、第二項は $\mathbf{x}$ がクリーンウェアの密集する領域にあるほど大きくなる。この $F(x)$ を小さくする（最小化する）ことが攻撃者の目的とする。また、True Labelの $y$ と検知器が導くラベル $y^c$ は区別して扱う。

バイナリ特徴量における $p(\mathbf{x} \mid y^c = \text{cleanware})$ はラプラシアンカーネル(もしくはRBFカーネル)を使えば良い。

$$$$ $$p(x \mid y^c = \text{cleanware}) = \frac{1}{n} \sum_{i=1}^n \exp \left(-\frac{\|\mathbf{x}-\mathbf{x}_i\|_1}{h}\right)$$

ここで、$\|\mathbf{x}-\mathbf{x}_i\|_1$ は $\mathbf{x}$ と $\mathbf{x}_i$ の $\ell_1$ ノルム（ハミング距離）であり、$n$ は検知器 $f$ がクリーンウェアと判定する(つまり$y^c = \text{cleanware}$となる)サンプルであり、攻撃者が推定のために用意できるサンプルの数である。すなわち、攻撃者の戦略は次のように置き換わる。

$$\arg \min_{\mathbf{x}} F(\mathbf{x}) = \hat{g}(\mathbf{x}) - \frac{\lambda}{n} \sum_{i | y_i^c = \text{cleanware}} k \left(\frac{\mathbf{x} - \mathbf{x}_i}{h}\right) \tag{2}$$ $$\text{s.t. } d(\mathbf{x}, \mathbf{x}^0) \leq d_{\max}, \tag{3}$$

直感的にいえば、 $F(x)$ を減少させるには、

(a) マルウェア分類器の出力するマルウェアスコア $g(x)$ を下げつつ

(b) $x$ をクリーンウェアサンプルの分布が高い領域（すなわち $p(\mathbf{x} \mid y^c = \text{cleanware})$ が高い領域に留まらせる

という2点を解決する必要がある。この密度項により、勾配降下法が導く方向は単に分類器を騙すだけではなく、「よりクリーンウェアに似せる」方向となる。その結果、生成された攻撃サンプルはモデルから見てより本物のクリーンウェアサンプルらしい特徴を持つようになり、検知をすり抜けやすくなる。

このアプローチは従来から知られるMimicry攻撃（正常動作の模倣攻撃）と同様に、攻撃対象のシステムに正常データを真似た痕跡を持ち込むことで検知を回避する効果がある。

そのため、以降ではこの項をmimicry componentと呼ぶ。

勾配降下の手順では、$F(x)$ の勾配 $\nabla F(x)$ を計算し、その反対方向へ少しずつ $\mathbf{x}$ を更新していく。$F(x)$ の定義から、勾配は

$$\nabla F(x) = \nabla g(\mathbf{x}) - \lambda \nabla p(\mathbf{x} \mid y^c = \text{cleanware})$$

となる。したがって、$\nabla g(x)$ が「よりマルウェアスコアを下げる方向」を示すのに対し、$\nabla p(\mathbf{x} \mid y^c = \text{cleanware})$ は「より良性データが多い領域へ向かう方向」を示す。

$\lambda$ によってこの二つのバランスが調整されることになる。$\lambda = 0$ なら従来通り分類器スコアだけを最小化し、$\lambda$が大きいほど「クリーンウェアらしさ」を重視した更新となる。結果として、「適切な $\lambda$」のもとで勾配降下法を用いると、攻撃サンプルは徐々に検知モデルの決定境界をすり抜けつつ、クリーンウェアのデータ分布に溶け込むような方向へ変化していく。この密度推定項は低密度領域にサンプルが迷い込むことを防ぐ一種の「ペナルティ項」として働くため、攻撃を加速させるものではない。勾配降下法が局所解に陥ったり不自然な解を見つけたりするのを緩和する。

ここでいう「適切な $\lambda$」は、$\nabla g(\mathbf{x})$ とのバランスを取れるように設定するべきであり、

$$\nabla p(\mathbf{x} \mid y^c = \text{cleanware}) = \frac{1}{nh} \sum_{i | y_i^c = -1} \exp\left(-\frac{\|\mathbf{x} - \mathbf{x}_i\|_1}{h}\right) (\mathbf{x} - \mathbf{x}_i)$$

であることから、$O(\frac{1}{nh})$ を考慮しなければならない。目的関数内の $\lambda$ の値を、 $\frac{\lambda}{nh}$ の値が識別関数 $\hat{g}(\mathbf{x})$ の値の範囲と同等（またはそれ以上）になるように選択する必要がある。

3. アルゴリズム

1. 初期設定: 攻撃対象のマルウェアサンプルを$\mathbf{x}^0$ とする。これが初めはモデルにマルウェアと分類されるポイントである。攻撃者は許容できる改変の範囲（例: 元のプログラムからの距離 $d_{\max}$）やステップサイズ $t$, 密度項の重み $\lambda$, 収束判定しきい値 $\epsilon$ を決定する
2. 勾配計算: 現在のサンプル $\mathbf{x}^m$ における損失関数 $F(\mathbf{x}^m) = g(\mathbf{x}^m) - \lambda p(\mathbf{x}^m \mid y^c = \text{cleanware})$ の勾配 $\nabla F(\mathbf{x}^m)$ を計算する。これは分類器の出力スコアに関する勾配と、クリーンウェアデータ密度の勾配を組み合わせたものである。$\nabla F(\mathbf{x}^m) = \nabla g(\mathbf{x}^m) - \lambda \nabla p(\mathbf{x}^m|y^c=\text{cleanware})$
3. サンプルの更新: $\mathbf{x}^m$を次のステップでは $\mathbf{x}^{m+1} = \mathbf{x}^m - t \cdot \nabla F(\mathbf{x}^m)$ と更新する。つまり、$\nabla F(x^m)$ の方向に沿ってステップサイズ $t$ だけサンプルを移動させる。この操作で分類器の出力スコアを下げつつ、クリーンウェア密度の高い方向へサンプルをわずかに変化させる。
4. 制約の適用: 更新後のサンプルが元のサンプルを超えてしまった場合、そのサンプルを許容範囲内に射影する
5. 反復と収束: 上記の勾配計算と更新を繰り返し行う。回避成功または変更量が収束判定しきい値 $\epsilon$ を下回った場合、ループを終了する。

引用: Evasion attacks against machine learning at test time(2013)